In mid-June I found myself standing on a rocky Portuguese shore gazing west into the blue expanse of the Atlantic Ocean. My GPS receiver dutifully placed me at a latitude of 37.2708˚ North and a longitude of 8.8607˚ West. Curiously, the Wren building on William & Mary’s campus is also located at 37.2708˚ North (and 76.7089˚ West). William & Mary is exactly due west of here. If I traveled straight west along the same line of latitude I’d reach campus after a journey of 5993 kilometers (3745 miles) and in the process would have traced out a small circle route.

Small circles are circles on spheres that don’t intersect the center of the sphere. Think of a round and ripe tomato- now cut the tomato to make slices suitable for a sandwich, the top and bottom of the slice form small circles. Lines of latitude are classic small circles, to circumnavigate the world at this latitude the journey would encompass some 31,800 kilometers, whereas at 89.99˚ North, about a kilometer or so south of the North Pole (90˚ North), circumnavigation would require a mere 7 kilometer traverse.
Alas there is a shorter route back to Williamsburg, that of the great circle route. Great circles are circles through spheres that do intersect the center of the sphere. Reflecting on tomatoes again, the tomato wedge, perfectly delectable in a salad, is an object edged by two great circles (half great circles actually). Lines of longitude are classic great circles. The great circle distance between the cliffs of Arrifana on the Portugal coast and Williamsburg is 5871 kilometers (3669 miles), shorter by over 100 kilometers (60 miles) than the small circle route. To travel back to Williamsburg along the great circle route, one would depart Portugal’s coast along a heading to the west-northwest, far out in the Atlantic we’d reach our most northerly point at nearly 43˚ North and then cross the Virginia shore inbound on a west-southwest heading.
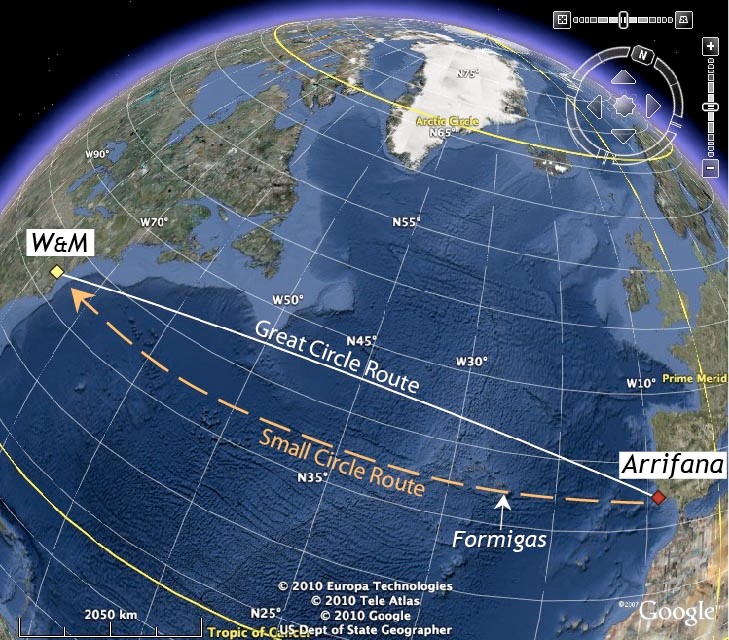
Long haul aviators and mariners are keen on great circle routes because, on our nearly spherical planet, they are the shortest distance between two points. Perhaps cutting a hundred or so kilometers off a journey of a few thousand seems no great savings, but consider traveling from Portugal’s west coast at 37.2708˚ North to the west coast of the United States at 37.2708˚ North (it’s Pescadero Beach in California), the great circle route is 800 kilometers shorter than the small circle route. A small circle journey across the Atlantic Ocean at 37.2708˚ North would not only be longer, but sailing on the sea you’d run smack into an exposed reef, Las Formigas (Portuguese for the ants), in the Azores archipelago!
I was in Portugal on holiday, but laid plans for starting geologic research here. There is much geology to be seen: folded Paleozoic rocks, Triassic red beds deposited at the birth of the Atlantic Ocean, Cretaceous igneous rocks, and mile after mile of remarkable coastline. It would be a spectacular setting for a geologic field course – we’ve offered field courses from Hawaii to Utah’s canyonlands, from California’s sierra to the Bahamas so why not throw Portugal in the mix.

This semester am teaching an introductory geology course, Geology 110-The Earth’s Environmental Systems. To understand the Earth system we must understand the basics about planet Earth and in this course we determine the Earth’s size and shape from first principles. Spatial relations are also vitally important – parallels, meridians, and great circle routes will become part of our lexicon and the always popular problem sets will be peppered with questions about navigation, in essence putting spatial relations to work by making observations. In the 15th century the Portuguese with their lateen-rigged caravels learned to navigate the seas far from land and started the age of discovery. This distant shore was a great place to ponder spatial relations and navigation, no doubt examples from Portugal and its Atlantic coast will appear throughout the course.
To explore these locales at 37.2708˚ North, download the Google Earth .kmz file.
Leave a Reply